题目分析
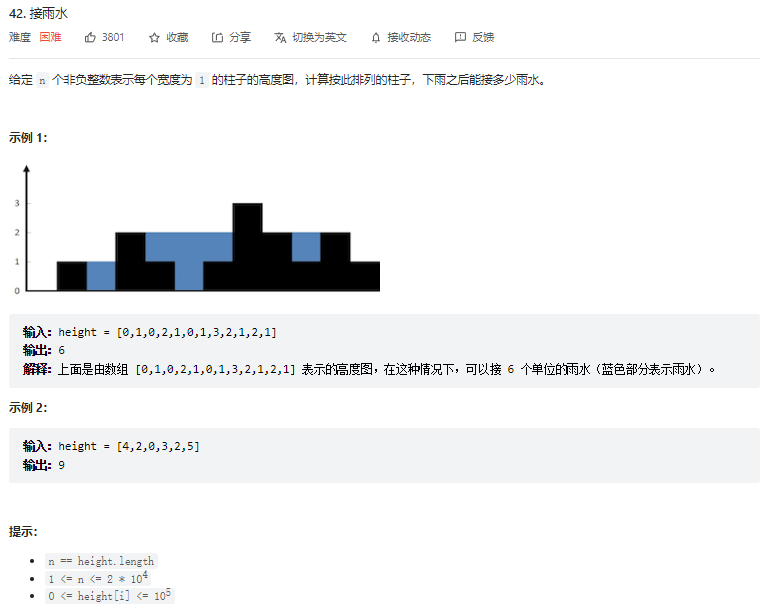
这个题目也是一个经典的算法题了,先简单给大家介绍一下题意,就是雨水类似于放在一个山谷里,如果左右都有高的地方,则可以放入水。本题有多种做法,小伙伴们可以先思考一下。
模拟
将这个这个一位数组表示成一个二维的地图,其中p(x, y)能放入水的要求是p(x, y)是空地,且p(m, y)和p(n, y)存在高点,其中m小于y,n大于y。
思路很明确,枚举每一个高度y,检查最左边L(m, y)和最右边的高点R(n, y),其中n和m中间的空地都是可以放入水滴的。
模拟方法虽然简单,但是会TLE。算法的**时间复杂度为O(mn),空间复杂度为O(1)**,n表示数组的长度,m表示数组的最大值。
1 | class Solution { |
动态规划
而且我们发现一个重要的性质“木桶效应”,一个木桶能放多少水,取决于最低的一块木板。对于本题二维来说,一个山谷能容纳多少水,也取决于左右最低的一边。
因此我们需要枚举每一个位置idx,找到左边和右边高度的最小值min,这个值决定了该位置能容纳多少水。如果min < height[idx],说明此处比两边还高,无法容纳水,否则可以容纳min - height[idx]数量的水。
我们对于每一个下标都去寻找了左边和右边的最高点,因此可以用两个数组保存左端和右端的最高值
$$ left[i] = max(left[i - 1], height[i - 1]) $$
$$ right[i] = max(right[i + 1], height[i + 1]) $$
算法的**时间复杂度为O(n),空间复杂度为O(n)**。
1 | class Solution { |
双指针
双指针是动态规划的空间优化解法,我们可以不按照从左到右的顺序遍历原数组。
我们思考一个问题,动态规划是不是要找到左右两端最大高度,然后求两端最大高度的最小值。
那么我们可以从左右两边开始遍历,如果左边的最小值小于等于右边的最大值,左边需要一直向右移动,因为决定该位置能放入多少雨水的是左边的最大值。并同时更新左边的最大值。
一旦左边出现了很高的位置,导致左边的最大值大于右边的最大值,则决定该位置能放入多少雨水的是右边的最大值。因此需要将右边不断向左移动,并同时更新右边的最大值。
算法的**时间复杂度为O(n),空间复杂度为O(1)**。
1 | class Solution { |
单调栈
单调栈的难度更大一些,一个元素如果小于等于其前面的元素,我们就继续遍历,因此栈是单调递减的。
如果当前元素大于栈顶的元素,那么说明前面的元素可以接水。
有一个特例,如果栈的尺寸为1,因为栈是单调递减的,说明除了要接水的位置(栈顶),前面没有更高的位置,因此该位置也不能接水。
如果栈的尺寸大于1,那么将要接水的高度m(栈顶)弹出后,新的栈顶n就是上一次高度大于等于m的值。
我们可以将高度补到n,再继续查看当前元素是否还大于新的栈顶n,如果还大于,则要将新的栈顶n弹出,更新的栈顶为p,则需要将水的高度补齐到p。
现在一个最最重要的问题就是,我们需要将m的位置也补齐到p,因为顺序是p、n、m,我们只将n的位置补齐到p是没用的,也需要将m的位置补齐到p。
举个例子,3、2、1、3,遍历到第二个3时,栈为[3, 2, 1],因为3大于栈顶1,因此要将1出栈,此时最新的栈顶为2,1可以放入水,放入的数量为2 - 1 = 1。然后继续看3仍然大于当前的栈顶2,则需要将2也出栈,此时最新的栈顶为3,2可以放入水、放入的数量是3 - 2 = 1,此时要注意,因为1已经补齐到2了,因此等价于3、2、2、3,此时两个2都需要放入水
所以我们在栈中不应该放入高度,而是应该放入索引,需要放入水的数量,就是当前位置 - 栈顶位置 - 1,放入水的高度就是新栈顶高度和当前高度的最小值 - 老栈顶的高度。
算法的**时间复杂度为O(n),空间复杂度为O(n)**。
1 | class Solution { |
刷题总结
本题除了第一种暴力算法,剩下的DP、双指针、单调栈都需要小伙伴能写出来。